
Above: Title page, volume 1, of Robert Dudley’s Dell’arcano del mare (1646), an encyclopedic work on navigation with an atlas of maps drawn on the Mercator projection. Image from Harvard University-Harvard Map Collection reproduced here under generous provisions of the Harvard Library Policy on Access to Digital Reproductions of Works in the Public Domain.
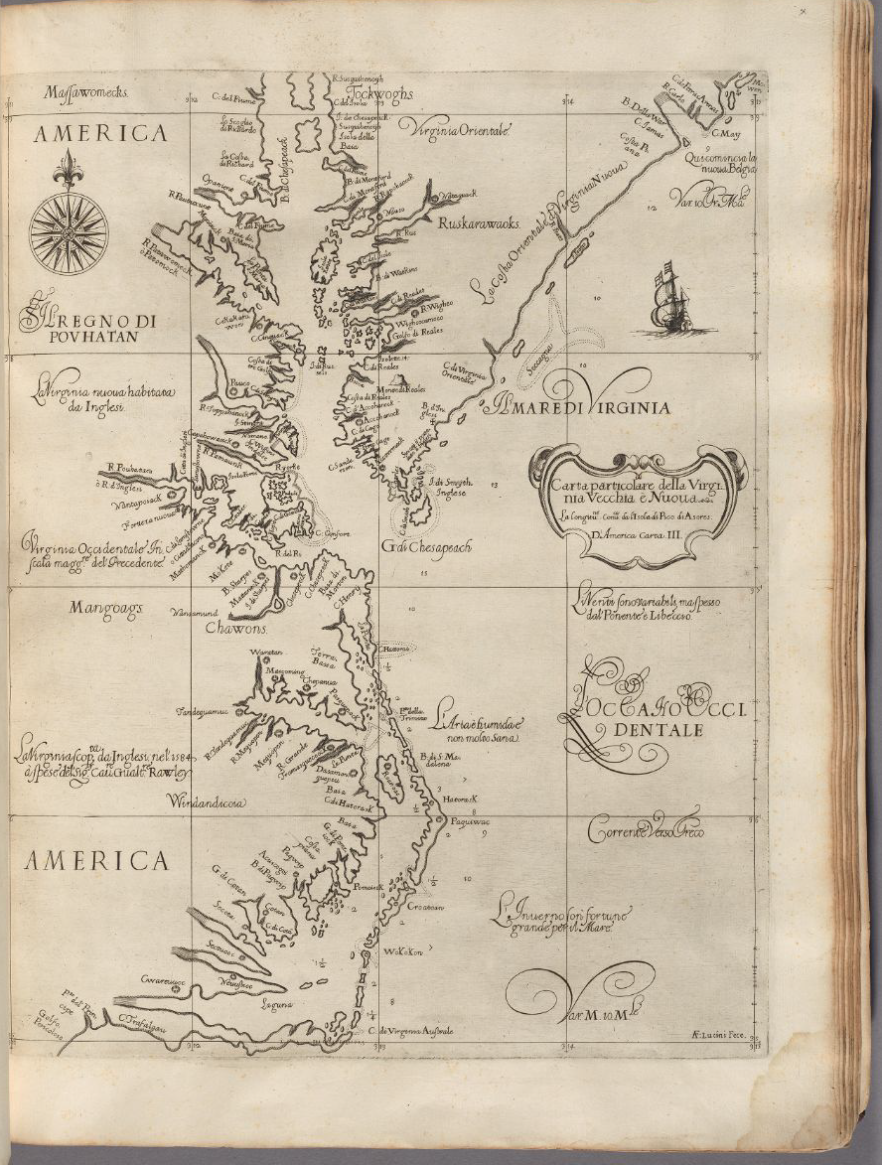
Title: Carta particolare della Virginia Vecchia è Nuoua
Internet Location: Harvard Library Viewer 44717498 seq 650
Description: This map, drawn on the Mercator projection, showed the Atlantic coast of North America from Delaware Bay in the upper right to Pamlico Sound in the lower left.
Source: Robert Dudley (1574-1649), Dell’arcano del mare, 3 volumes, Florence: Francesco Onofri, 1646-1647. Volume 3. Image from Harvard University-Harvard Map Collection reproduced here under generous provisions of the Harvard Library Policy on Access to Digital Reproductions of Works in the Public Domain. Further bibliographical description available in the Hollis Online Catalog of Harvard Library.
Comment:
(1) The Mercator Projection
This map of “Virginia” numbered among the first maps of smaller areas of the earth to be drawn on the projection that Gerardus Mercator used for his world map of 1569. A navigator using a Mercator map can mark a straight line between any two points on the map, and that line will describe a true compass bearing. (Such a straight line will not usually describe the shortest distance between two points on the earth’s surface. The shortest distance is a “great circle” or circumference and, typically, must be plotted on a Mercator map as a series of straight lines to make up a curve on the map.)
The power of the Mercator projection consisted mainly in its great navigational advantage over other projections. Its propagandistic power for European imperialism—its increase of Europe’s size in the map space at the expense of Africa and other equatorial continents—took a distant second place in history to its navigational power for guiding Europeans, European navies, European trade, and European values across oceans to the rest of the world.
Mercator maps set east-west grid lines (latitude) at right angles to north-south (longitude) grid lines.
Mercator maps stretch out lines of latitude so that they are all equal to the equator. A line of latitude near the North Pole is the same length in the map space as the equator. On a globe or a sphere, these lines would have very different lengths.
Also unlike a globe, Mercator maps set lines of longitude parallel to each other and equally spaced from each other. Mercator maps do preserve the equal lengths of longitude on a globe.
However, the distance along a line of longitude between the equator and, say, 10º North latitude is much smaller in the map space than the distance between 70º and 80º. So, on modern Mercator maps, Greenland occupies almost as much map space as Africa, which is very misleading. But the increasing distance in the map space between the same number of degrees of latitude as the eye moves up (north) or down (south) along a line of longitude preserves true compass directions at any given point.
Mercator maps also preserve the shapes of geographical features in a local area even though they distort comparative sizes in large areas.
(2) English Work on the Mercator Projection during the 16th Century
The working out of the mathematics for constructing a Mercator map, which had to be accomplished in order to make maps of practical value at sea, took many years, and it required the invention of logarithms. Mercator seems to have summarized his own knowledge in a diagram in the lower right corner of his 1569 world map, but, as far as anyone knows today, he never drew maps of smaller areas of the world using his new projection.
Thomas Harriot, who was involved in Walter Raleigh’s voyages to the Americas, derived tables of “meridional parts” that, for a given latitude in the map space, returned distance from the equator along a line of longitude in the map space. Edward Wright published such a table in 1599. Even before Harriot, John Dee studied with Mercator and worked on the problem in his unpublished Canon Gubernauticus (1558). In a discourse on the Northwest Passage published in Richard Hakluyt’s The Principal Navigations, Voyages, Traffiques and Discoveries of the English Nation (1598-1600), Humphrey Gilbert claimed to have addressed it.
(3) Robert Dudley’s Sources
Robert Dudley’s Dell’arcano del mare included the first published Mercator maps of practical navigational value because he mapped much smaller areas than Mercator’s map of the entire world. To what extent did Dudley use and rely on the work of earlier English mathematicians and navigators?
Sarah Tyacke has studied this and related questions. Some of her scholarship, as of 2007, appeared in The History of Cartography, ed. J. B. Harley, David Woodward, and others, 6 vols., Chicago: The University of Chicago Press, 1987-, 3: 1722-1753, especially 1733, 1739, available in PDF at http://www.press.uchicago.edu/books/HOC/index.html.
Dudley collected sea charts (nautical charts), and the Bayerische StaatsBibliothek in Munich has digitized manuscript books related to Dell’arcano del mare at
https://opacplus.bsb-muenchen.de/search?oclcno=802566595&db=100
https://opacplus.bsb-muenchen.de/search?oclcno=802566755&db=100
https://opacplus.bsb-muenchen.de/search?oclcno=802566393&db=100
https://opacplus.bsb-muenchen.de/search?oclcno=802566867&db=100
Images of some of Dudley’s navigational instruments bequeathed, after a long exile from England, to the Medici in Florence appear at
http://catalogue.museogalileo.it/multimedia/DudleyCollection.html
(4) Centerless Space
What understanding of space lay behind English work on the Mercator projection?
Unlike medieval European maps of the world that focused on Jerusalem or narrative maps, the space of the Mercator map and the terrestrial space it was supposed to represent had no center.
Empires are often analyzed in terms of a center (London) and a periphery (Virginia). But the Mercator map enabled its users to visualize any point as a “center,” what the earth would look like at that point, and what would lie in any given direction from that point. It gave its users information about moving to or from that point for whatever purpose they could imagine or desire.
The concept of space underlying Dudley’s Virginia map and his other maps in Dell’arcano del mare emphasized geometric continuity throughout the earth. Does this have any similarity to the mathematical conception of space in the physics of Galileo Galilei, who worked in Florence under the patronage of the Medici at the same time as Robert Dudley?